1º Tarea (La práctica de ordenador). Cuando terminéis la práctica mandarme un correo a pcampillo@goumh.umh.es
2º Había un ejercicio de métodos numéricos. Hay que mandar los resultados a pcampillo@goumh.umh.es
3º Había otro ejercicio de métodos numéricos. Hay que mandar los resultados a pcampillo@goumh.umh.es
4º Sobre lo de hacer un post, de momento es imposible, no están funcionando las cuentas goumh, para hacer blog. "de momento".
martes, 28 de diciembre de 2010
domingo, 26 de diciembre de 2010
lunes, 20 de diciembre de 2010
2º Parcial Corregido Parcial del 18-12-2010
Los alumnos que quieran ver, recoger el 2º Parcial, estaré en mi despacho a a partir de las 11:20
jueves, 16 de diciembre de 2010
Las soluciones que me salen de los ejercicios CUIDADO HOJA RECTIFICADA
1º Ejercicio Solución 6'8 segundos
2º Ejercicio Solución 172 segundos
3º Nota la función que definía la región estaba equivocada en la hoja y la he tenido que cambiar
Solución 0,533
4º Solución 0'183
5º Rectificación en la función para que tome valores positivos
Mediana 1º Paso 4, 2º Paso 5.5
Trapecio 1º Paso 10, 2º Paso 7
NOTA: He hecho los ejercicios, pero puede ser que me haya equivocado (suele ser habitual)
2º Ejercicio Solución 172 segundos
3º Nota la función que definía la región estaba equivocada en la hoja y la he tenido que cambiar
Solución 0,533
4º Solución 0'183
5º Rectificación en la función para que tome valores positivos
Mediana 1º Paso 4, 2º Paso 5.5
Trapecio 1º Paso 10, 2º Paso 7
NOTA: He hecho los ejercicios, pero puede ser que me haya equivocado (suele ser habitual)
Clases del Miércoles 15 de Diciembre y Jueves 16 de Diciembre
Las clases del Miércoles 15 de Diciembre y Jueves 16 de Diciembre
Han sido talleres de ejercicios para preparar el 2º Parcial de la asignatura.
Han sido talleres de ejercicios para preparar el 2º Parcial de la asignatura.
miércoles, 15 de diciembre de 2010
PLES
El Martes pasado estuve en las Jornadas de Inovación docente de la UMH. Y Jordi Adell nos hablo de los PLES, os dejo un vídeo de 10 minutos.
A lo mejor esta navidad hacemos algo de esto ????
Cuando digo hacemos, me refiero a alumnos y profesor.
TEMA PRACTICAS ORDENADOR
A medida que vayáis terminado las prácticas de ordenador, ir enviándome un correo a pcampillo@goumh.umh.es que vaya corrigiendo.
viernes, 10 de diciembre de 2010
Versión 0.1 Parcial
Primera parte
1º Complejo
2º Problema de métodos numéricos.
3º Diagonalización de matrices.
Segunda parte
4º Factorización LU
5º Problema de ecuaciones diferenciales
6º Calculo de Área o Volúmenes mediante integrales
7º Integrales dobles o Integrales Triples
1º Complejo
2º Problema de métodos numéricos.
3º Diagonalización de matrices.
Segunda parte
4º Factorización LU
5º Problema de ecuaciones diferenciales
6º Calculo de Área o Volúmenes mediante integrales
7º Integrales dobles o Integrales Triples
Clase del 10 de Diciembre del 2010
Métodos numéricos
Calculo de Integrales mediante metodos númericos
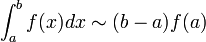
Regla del rectángulo
El método más simple de este tipo es hacer a la función interpoladora ser una función constante (un polinomio de orden cero) que pasa a través del punto (a,f(a)). Este método se llama la regla del rectángulo:Regla del punto medio
Si en el método anterior la función pasa a través del punto
regla del punto medio:
Regla del trapecio
La función interpoladora puede ser una función afín (un polinomio de grado 1 o sea una recta) que pasa a través de los puntos 
regla del trapecio:
regla del trapecio:
Regla de Simpson
La función interpoladora puede ser un polinomio de grado 2 que pasa a través de los puntos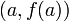 
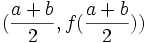
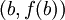
Ejercicio para hacer y entregar
intervalo [0,2] , por todos los métodos estudiados, primero con un solo intervalo, y después haciendo dos intervalos.Enviar los resultados a pcampillo@goumh.umh.es
jueves, 9 de diciembre de 2010
Clase del 9 de Diciembre del 2010 Métodos numéricos
Métodos numéricos
La disciplina ocupada de describir, analizar y crear algoritmos numéricos que nos permitan resolver problemas matemáticos, en los que estén involucradas cantidades numéricas
En el contexto del cálculo numérico, un algoritmo es un procedimiento que nos puede llevar a una solución aproximada de un problema mediante un número finito de pasos que pueden ejecutarse de manera lógica.
A partir de aquí, aparece un concepto adicional, el de error.
Búsqueda de raíces
En análisis numérico un algoritmo de búsqueda de raíces es un método numérico o algoritmo para encontrar las soluciones aproximadas de una ecuación dada por la expresión f(x) = 0 para una función matemática f dada. A la solución x de la ecuación se le llama raíz o cero de la función.
El algoritmo más simple de búsqueda de raíces es el método de bisección. Requiere un intervalo inicial que contenga alguna raíz de la ecuación (de forma que la función tome en los extremos del mismo valores de distinto signo; véase el teorema de Bolzano). Dicho intervalo inicial se va dividiendo sucesivamente por la mitad (se bisecta) tomándose el intervalo que contiene a la raíz. A pesar de ser un método que siempre converge a una solución, converge muy lentamente.
http://es.wikipedia.org/wiki/M%C3%A9todo_de_bisecci%C3%B3n
Ejemplo función:
f(x)=x^2-1 Entre el 0 y 3
Ejemplo función:
f(x)=x^2+x-1 Entre 0 y 1
Es un algoritmo seguro pero lento
Uno mejor: Método de Newton
http://es.wikipedia.org/wiki/M%C3%A9todo_de_Newton
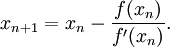
Ejemplo función
f(x)=x^2-1 Entre el 0 y 3
Ejemplo función
f(x)=x^2+x-1 Entre 0 y 1
La disciplina ocupada de describir, analizar y crear algoritmos numéricos que nos permitan resolver problemas matemáticos, en los que estén involucradas cantidades numéricas
En el contexto del cálculo numérico, un algoritmo es un procedimiento que nos puede llevar a una solución aproximada de un problema mediante un número finito de pasos que pueden ejecutarse de manera lógica.
A partir de aquí, aparece un concepto adicional, el de error.
Búsqueda de raíces
En análisis numérico un algoritmo de búsqueda de raíces es un método numérico o algoritmo para encontrar las soluciones aproximadas de una ecuación dada por la expresión f(x) = 0 para una función matemática f dada. A la solución x de la ecuación se le llama raíz o cero de la función.
El algoritmo más simple de búsqueda de raíces es el método de bisección. Requiere un intervalo inicial que contenga alguna raíz de la ecuación (de forma que la función tome en los extremos del mismo valores de distinto signo; véase el teorema de Bolzano). Dicho intervalo inicial se va dividiendo sucesivamente por la mitad (se bisecta) tomándose el intervalo que contiene a la raíz. A pesar de ser un método que siempre converge a una solución, converge muy lentamente.
http://es.wikipedia.org/wiki/M%C3%A9todo_de_bisecci%C3%B3n
Ejemplo función:
f(x)=x^2-1 Entre el 0 y 3
Ejemplo función:
f(x)=x^2+x-1 Entre 0 y 1
Es un algoritmo seguro pero lento
Uno mejor: Método de Newton
http://es.wikipedia.org/wiki/M%C3%A9todo_de_Newton
Ejemplo función
f(x)=x^2-1 Entre el 0 y 3
Ejemplo función
f(x)=x^2+x-1 Entre 0 y 1
lunes, 6 de diciembre de 2010
Practicas de Ordenador
Os recomiendo que abráis el documento que podéis encontrar pinchando en BORRADOR y que lo seleccionéis todo y lo copiéis en otro documento propio.
El otro documento debe de ser un Google Doc,
Para ello entrar en docs.goumh.umh.es
Os pedirá vuestro nombre de usuario y contraseña, tenéis que hacer lo mismo que habéis hecho habitualmente en Clase de Informática.
Vuestro nombre de usuario es (lo que hay delante de la arroba, de vuestro correo de la universidad) y vuestra clave, es el PIN que os dieron al realizar la matricula.
Es entonces cuando tenéis que hacer un documento nuevo en Google Doc, donde haréis la practica.
En ese documento copiareis lo que poner en el documento BORRADOR para facilitar el copiar os digo los comandos que debéis de utilizar.
Ctrl+A para seleccionar todo el documento
Ctrl+C para copiar
Ctrl +V para pegar
Después tenéis que compartir el documento con pcampillo@goumh.umh.es
Las practicas estan divididas en 2 ejercicios.
El primero se basa en las características que tiene Google como calculadora y conversor
El segundo se basa en las posibilidades de Wolfranalpha como asistente matemático.
El otro documento debe de ser un Google Doc,
Para ello entrar en docs.goumh.umh.es
Os pedirá vuestro nombre de usuario y contraseña, tenéis que hacer lo mismo que habéis hecho habitualmente en Clase de Informática.
Vuestro nombre de usuario es (lo que hay delante de la arroba, de vuestro correo de la universidad) y vuestra clave, es el PIN que os dieron al realizar la matricula.
Es entonces cuando tenéis que hacer un documento nuevo en Google Doc, donde haréis la practica.
En ese documento copiareis lo que poner en el documento BORRADOR para facilitar el copiar os digo los comandos que debéis de utilizar.
Ctrl+A para seleccionar todo el documento
Ctrl+C para copiar
Ctrl +V para pegar
Después tenéis que compartir el documento con pcampillo@goumh.umh.es
Las practicas estan divididas en 2 ejercicios.
El primero se basa en las características que tiene Google como calculadora y conversor
El segundo se basa en las posibilidades de Wolfranalpha como asistente matemático.
Clase del 2-12-2010 Viernes
Ejemplo de calculo del Área de una función entre dos curvas. Integrales de 1 variable
Ejemplo de Integral de una función de dos variables sobre un recinto, Integrales dobles. Calculo del Volumen
Ejemplo de Integrales triples.
Practicas en el aula de Informática
Ejemplo de Integral de una función de dos variables sobre un recinto, Integrales dobles. Calculo del Volumen
Ejemplo de Integrales triples.
Practicas en el aula de Informática
miércoles, 1 de diciembre de 2010
lunes, 29 de noviembre de 2010
IMPORTANTE PRACTICAS RECOMENDACIONES
RECOMENDACIONES: Os recomiendo que abráis el documento que podéis encontrar pinchando en BORRADOR, y que lo seleccionéis todo y lo copiéis en otro documento propio.
El otro documento puede ser un Google Doc, un Documento de Open Office, y también es posible en un documento de WORD.
Así podréis ir rellenando con facilidad los datos que va pidiendo la práctica.
Esta semana tenemos prácticas de Ordenador
Los grupos se tienen que distribuir entre el Jueves y el Viernes, aunque también puede empezar a hacer la hoja de prácticas en casa.
Aquí os dejo una versión BORRADOR.
El otro documento puede ser un Google Doc, un Documento de Open Office, y también es posible en un documento de WORD.
Así podréis ir rellenando con facilidad los datos que va pidiendo la práctica.
Esta semana tenemos prácticas de Ordenador
Los grupos se tienen que distribuir entre el Jueves y el Viernes, aunque también puede empezar a hacer la hoja de prácticas en casa.
Aquí os dejo una versión BORRADOR.
Clase del Viernes 26 de Noviembre del 2010
El Viernes vimos como calcular alguna Área más, y como calcular Volumenes de revolución.
El culmen fue: el calculo de cuanto había que rellenar una copa de champan, para que le tuviera la mitad del volumen.
El culmen fue: el calculo de cuanto había que rellenar una copa de champan, para que le tuviera la mitad del volumen.
jueves, 25 de noviembre de 2010
Clase del Miércoles 24 de Noviembre y Jueves 25 de Noviembre del 2010
Día 24 de Noviembre
Reparto del parcial corregido.
Comienzo de las integrales definidas, con partición de un intervalo, y Regla de Barow.
Ejemplo de función no integrable.
Día 25 de Noviembre
Integrales definidas. Calculo de Áreas
Reparto del parcial corregido.
Comienzo de las integrales definidas, con partición de un intervalo, y Regla de Barow.
Ejemplo de función no integrable.
Día 25 de Noviembre
Integrales definidas. Calculo de Áreas
miércoles, 24 de noviembre de 2010
EPSO BETATESTER
Estamos intentando compartir un documento, para que solo lo puedan ver los alumnos matriculados en la asignatura.
El documento que tenéis compartido es la Resolución de examen Parcial.
Para poder verlo tenéis que hacer caso a unos correos que os ha enviado Marco a vuestra dirección de correo electrónico de la Universidad.
Esta mañana no funcionaba, pero en estos momentos ya funciona.
Os pido que todos los que lo intentes, dejéis aquí algún comentario, sobre como os ha ido.
El documento que tenéis compartido es la Resolución de examen Parcial.
Para poder verlo tenéis que hacer caso a unos correos que os ha enviado Marco a vuestra dirección de correo electrónico de la Universidad.
Esta mañana no funcionaba, pero en estos momentos ya funciona.
Os pido que todos los que lo intentes, dejéis aquí algún comentario, sobre como os ha ido.
martes, 23 de noviembre de 2010
Clase del Jueves 18-11-2010 , Viernes 19-11-2010
Jueves clase de problemas de repaso para el parcial del Viernes
Viernes Parcial en dos partes.
1ª Parte
Números Complejos
Factorización LU con aplicaciones
Límite de funciones de dos variables
2ª Parte
Ecuaciones Diferenciales (apareció un problema de movimiento, caída de una bola)
Diagonalización de una matriz
Máximos y Mínimos de una función de 3 variables.
Viernes Parcial en dos partes.
1ª Parte
Números Complejos
Factorización LU con aplicaciones
Límite de funciones de dos variables
2ª Parte
Ecuaciones Diferenciales (apareció un problema de movimiento, caída de una bola)
Diagonalización de una matriz
Máximos y Mínimos de una función de 3 variables.
miércoles, 17 de noviembre de 2010
Clase del Miércoles 17-11-2010
Clase de problemas de repaso
Y Números complejos
- Factorización LU con aplicación en la resolución de un sistema de ecuaciones.
Y Números complejos
- División
- Producto en forma modulo argumento
- Raíces.
viernes, 12 de noviembre de 2010
Clases de la semana Integración y Ecuaciones Diefrenciales
Miércoles clase de 8:30 a 9:30
Jueves Clase de 8:30 a 9:30
Viernes Clase de 8:30 a 9:30
Hemos presentado que saldrá en el primer parcial.
1º) Factorización LU con aplicación a la resolución de un sistema de ecuaciones lineales
2º) Diagonalización de matrices (1º Valores y vectores propios)
3º) Máximos y Mínimos de funciones de 2 variables.
4º) Números complejos
5º) Problemas de ecuaciones diferenciales
En clase hemos visto ejemplos, y integrales inmediatas.
Y problemas de ecuaciones diferenciales de:
1º Poblaciones
2º Movimiento (caída de piedras)
3º Enfriamiento y calentamiento de cuerpos
4º Mezclas
Jueves Clase de 8:30 a 9:30
Viernes Clase de 8:30 a 9:30
Hemos presentado que saldrá en el primer parcial.
1º) Factorización LU con aplicación a la resolución de un sistema de ecuaciones lineales
2º) Diagonalización de matrices (1º Valores y vectores propios)
3º) Máximos y Mínimos de funciones de 2 variables.
4º) Números complejos
5º) Problemas de ecuaciones diferenciales
En clase hemos visto ejemplos, y integrales inmediatas.
Y problemas de ecuaciones diferenciales de:
1º Poblaciones
2º Movimiento (caída de piedras)
3º Enfriamiento y calentamiento de cuerpos
4º Mezclas
jueves, 11 de noviembre de 2010
viernes, 5 de noviembre de 2010
Clase del Viernes del 5-11-2010 (Taller de problemas) de 8:30 a 9:30
1º Problema
Calcula los avalores y vectores propios de la matriz:
Despues diagonaliza la matriz
2º Ejercicio de matriz de 3x3, con dos valores propios, y 3 vectores propios, para diagonalizar la matriz.
3º Ejercicio Derivada de una función de 2 variables.
4º Ejercicios Derivada de una función de 2 variables.
Calcula los avalores y vectores propios de la matriz:
Despues diagonaliza la matriz
2º Ejercicio de matriz de 3x3, con dos valores propios, y 3 vectores propios, para diagonalizar la matriz.
3º Ejercicio Derivada de una función de 2 variables.
4º Ejercicios Derivada de una función de 2 variables.
jueves, 4 de noviembre de 2010
Clase del Jueves DIagonalización de matrices
La parte final del vídeo que pusimos el día anterior, y los diez primeros minutos de este vídeo.
miércoles, 3 de noviembre de 2010
lunes, 1 de noviembre de 2010
2º Clase del Viernes 29-10-2010
Introducción a las aplicaciones lineales
Ejemplo
Ver la linealidad.
Calculo del espacio nulo.
Diferentes ejemplos.
Ejemplo
Ver la linealidad.
Calculo del espacio nulo.
Diferentes ejemplos.
1ª Clase de Viernes 29-10-2010
Recuerdos del calculo de Máximos y Mínimos de funciones de una variable
Procedimiento para el calculo de extremos de funciones de dos variables
1º Derivadas parciales
2º Igualamos a cero, conseguimos los puntos candidatos
3º Derivadas segundas Matriz Hessiana
4º "hessianitos" para saber que tipo de punto es cada punto candidato
Procedimiento para el calculo de extremos de funciones de dos variables
1º Derivadas parciales
2º Igualamos a cero, conseguimos los puntos candidatos
3º Derivadas segundas Matriz Hessiana
4º "hessianitos" para saber que tipo de punto es cada punto candidato
jueves, 28 de octubre de 2010
Clase de Álgebra del 28-10-2010
Recordatorio.
Ejemplo de resolución de un sistema de ecuaciones lineales, resolviéndolo por el método de Gauss-Jordan.
Diferentes sistemas de ecuaciones lineales, ya presentados como matriz escalonada por filas reducida, calculo de la solución.
Método de Gauss Jordan para el calculo de la inversa de una matriz.
Ejemplo de una matriz invertible, y de una matriz no invertible.
Determinantes.
Como se calcula las inversas de matrices cuadradas. Para matrices de 1x1, 2x2, 3x3.
Ejemplo de resolución de un sistema de ecuaciones lineales, resolviéndolo por el método de Gauss-Jordan.
Diferentes sistemas de ecuaciones lineales, ya presentados como matriz escalonada por filas reducida, calculo de la solución.
Método de Gauss Jordan para el calculo de la inversa de una matriz.
Ejemplo de una matriz invertible, y de una matriz no invertible.
Determinantes.
Como se calcula las inversas de matrices cuadradas. Para matrices de 1x1, 2x2, 3x3.
Clase del Miércoles 27-Octubre del 2010 Límites de dos variables.
Ejemplos de límites de funciones por caminos
Cambio a polares
Ejemplos de límites de funciones, haciendo límites por caminos, y límites por cambio a polares.
Cambio a polares
Ejemplos de límites de funciones, haciendo límites por caminos, y límites por cambio a polares.
miércoles, 27 de octubre de 2010
FECHA DEL PRIMER PARCIAL 19 de Noviembre del 2010
La fecha para el primer parcial de Matemáticas es el 19 de Noviembre del 2010, a las 11:00
domingo, 24 de octubre de 2010
Clases del Viernes 22-10-2010
No disponemos de Presentaciones de estas Clases.
1º Hora de las 8:30 a 9:30
TALLER DE DERIVADAS, ejercicios de derivadas de una variable, y de dos variables.
2º Hora de las 11:00 hasta la finalización de la clase
Recuerdo de la definición de función de 1a variable y de dos variables.
Ideas simples, y problemas de comprensión, derivados de la palabra tangente al aplicarla a la derivada.
Y problemas con la palabra continuidad.
Definición de Límite (representación gráfica),y explicación mediante bandas.
Ejemplo de función sin límite en un punto y por tanto discontinua sen(1/x)
Ejemplos de Límites de una variable muy fáciles de calcular.
Límites por caminos, en funciones de 2 variables.
1º Hora de las 8:30 a 9:30
TALLER DE DERIVADAS, ejercicios de derivadas de una variable, y de dos variables.
2º Hora de las 11:00 hasta la finalización de la clase
Recuerdo de la definición de función de 1a variable y de dos variables.
Ideas simples, y problemas de comprensión, derivados de la palabra tangente al aplicarla a la derivada.
Y problemas con la palabra continuidad.
Definición de Límite (representación gráfica),y explicación mediante bandas.
Ejemplo de función sin límite en un punto y por tanto discontinua sen(1/x)
Ejemplos de Límites de una variable muy fáciles de calcular.
Límites por caminos, en funciones de 2 variables.
jueves, 21 de octubre de 2010
miércoles, 20 de octubre de 2010
Clase del día 20-10-2010 Álgebra Lineal
Repasamos lo que habíamos dado de Matrices elementales
Presentación
Llegando hasta que se puede calcular la Inversa como producto de matrices elementales
Pasamos a ver las inversas de las Matrices elementales
Ejercicios, buscando la matriz elemental.
Después pasamos a ver la Factorización LU, con un ejemplo. Llegamos a la factorización LU
(esta presentación todavía no esta hecha)
Presentación
Llegando hasta que se puede calcular la Inversa como producto de matrices elementales
Pasamos a ver las inversas de las Matrices elementales
Ejercicios, buscando la matriz elemental.
Después pasamos a ver la Factorización LU, con un ejemplo. Llegamos a la factorización LU
(esta presentación todavía no esta hecha)
lunes, 18 de octubre de 2010
Necesidad de una cuenta de GMAIL
Se necesita que todos los alumnos dispongan de una cuenta de GMAIL.
Por lo que tendréis que haceros una en Gmail.
Mi recomendación, es que cojáis un nombre que pueda ser reconocible, y que sea un correo que nos os de vergüenza dar, cuando en un futuro lo necesitéis para algo serio.
Ejemplo: como se pueden utilizar, nombres con puntos, se podría poner algo como:
pepito.perez.umh@gmail.com
Cuando dispongáis de una cuenta de Gmail.
Tendréis que pinchar en este enlace, y meter esa cuenta para que a mi me aparezca en el listado de alumnos con cuenta de GMAIL.
Para ello lo primero que te pedirá sera el usuario: (para ello tienes que recordar tu dirección de la UMH, que debería ser algo así como pepito.perez@umh.es) Pues tu usuario sera pepito.perez
Y tu clave sera el pin de 6 Números que utilizas para identificarte en la UMH, y que es el que te dieron al hacer la matricula.
Después de identificarte pasaras a una pantalla donde tendrás que poner la dirección de GMAIL
Por lo que tendréis que haceros una en Gmail.
Mi recomendación, es que cojáis un nombre que pueda ser reconocible, y que sea un correo que nos os de vergüenza dar, cuando en un futuro lo necesitéis para algo serio.
Ejemplo: como se pueden utilizar, nombres con puntos, se podría poner algo como:
pepito.perez.umh@gmail.com
Cuando dispongáis de una cuenta de Gmail.
Tendréis que pinchar en este enlace, y meter esa cuenta para que a mi me aparezca en el listado de alumnos con cuenta de GMAIL.
Para ello lo primero que te pedirá sera el usuario: (para ello tienes que recordar tu dirección de la UMH, que debería ser algo así como pepito.perez@umh.es) Pues tu usuario sera pepito.perez
Y tu clave sera el pin de 6 Números que utilizas para identificarte en la UMH, y que es el que te dieron al hacer la matricula.
Después de identificarte pasaras a una pantalla donde tendrás que poner la dirección de GMAIL
viernes, 15 de octubre de 2010
Clase de Álgebra del 15-10-2010
Presentación de Matrices elementales.
Se propusieron también 3 ejercicios de búsqueda de las matrices elementales correspondientes.
Se propusieron también 3 ejercicios de búsqueda de las matrices elementales correspondientes.
Solucionar problemas (PARA LOS QUE NO VEAN BIEN ESTE BLOG)
Los problemas de este Blog, pueden ser debidos a:
1º No disponeis de una versión de Adobe Reader actualizada. Solución bajarse e instalar la ultima versión de Adobe Reader.
2º No tenéis un navegador actualizado. Solución bajarse la ultima versión de Firefox, o de Google Crome.
1º No disponeis de una versión de Adobe Reader actualizada. Solución bajarse e instalar la ultima versión de Adobe Reader.
2º No tenéis un navegador actualizado. Solución bajarse la ultima versión de Firefox, o de Google Crome.
jueves, 14 de octubre de 2010
Clase de funciones 14-10-2010
En esta hemos presentado las funciones de 1 variable, y de 2 variable, así como el calculo de derivadas
Presentación Funciones de 1 Variable
Presentación funciones de 2 variables
Boceto de la presentación de Calculo de derivadas
Presentación Funciones de 1 Variable
Presentación funciones de 2 variables
Boceto de la presentación de Calculo de derivadas
miércoles, 13 de octubre de 2010
sábado, 9 de octubre de 2010
Números Complejos clase del 8-10-10
Repaso de ejercicios de Nº Complejos
1º Suma, producto y cociente
2º Pasar números complejos expresados en forma binomica a forma polar
3º Producto de números de forma polar
4º Potencias de números complejos
5º Raíces de números complejos
(No disponemos de presentación)
(Se puede seguir el libro que se puso como modelo en la anterior clase)
1º Suma, producto y cociente
2º Pasar números complejos expresados en forma binomica a forma polar
3º Producto de números de forma polar
4º Potencias de números complejos
5º Raíces de números complejos
(No disponemos de presentación)
(Se puede seguir el libro que se puso como modelo en la anterior clase)
2º Clase de Álgebra Lineal 8-10-2010
Presentaciones:
Alguna Bibliografía en Español
Sistemas de ecuaciones lineales Introduccion al Algebra Lineal Howard
Eliminacion Gaussiana Introduccion al Algebra Lineal Howard Anton pg29-pg43.pdf
Alguna Bibliografía en ingles
The Idea of Elimination Cap 2.2 Introduction to Linear Algebra Gilbert
Elimination using matrices Cap 2.3 Introduction to Linear Algebra Gilbert
jueves, 7 de octubre de 2010
1ª Clase de Álgebra Lineal 7-10-2010
Introducción al Álgebra lineal
Lo más interesante de esta clase es la representación de los sistemas de ecuaciones lineales, como columnas.
Combinaciones lineales de columnas.
Álgebra Lineal Idea de eliminación
Texto en los que se basan las presentaciones:
Libro Algebra Cap 1 (vectores)
Libro Algebra Cap 2.1 Introducción al Álgebra
http://ocw.mit.edu/courses/mathematics/18-06-linear-algebra-spring-2010/video-lectures/lecture01/
Lo más interesante de esta clase es la representación de los sistemas de ecuaciones lineales, como columnas.
Combinaciones lineales de columnas.
Álgebra Lineal Idea de eliminación
Texto en los que se basan las presentaciones:
Libro Algebra Cap 1 (vectores)
Libro Algebra Cap 2.1 Introducción al Álgebra
http://ocw.mit.edu/courses/mathematics/18-06-linear-algebra-spring-2010/video-lectures/lecture01/
miércoles, 6 de octubre de 2010
2º Clase de Números Complejos 6-10-2010
Necesidad de ampliación de los Números complejos Presentación Parte 2
Presentación Parte 3
Operaciones con Números complejos Presentación 4
Forma Polar de un Número complejo Presentación 5
Presentación Parte 3
Operaciones con Números complejos Presentación 4
Forma Polar de un Número complejo Presentación 5
miércoles, 29 de septiembre de 2010
Números Complejos
Documento para dudas de Números complejos <---- Aquí podéis escribir vuestras dudas, este es un documento que se puede editar por los alumnos.
1ª Clase de Números Complejos del 29-9-2010
Algo de Historia, y la demostración de la irracionalidad de raíz de 2
Algo de Bibliografía:
Número Complejos Matematicas 1 Ed Bruño pg 26-30.pdf
Número Complejos Matematicas 1 Ed Bruño pg 122-127.pdf
Número Complejos Introduction to Linear Algebra Gilbert Strang
1ª Clase de Números Complejos del 29-9-2010
Algo de Historia, y la demostración de la irracionalidad de raíz de 2
Algo de Bibliografía:
Número Complejos Matematicas 1 Ed Bruño pg 26-30.pdf
Número Complejos Matematicas 1 Ed Bruño pg 122-127.pdf
Número Complejos Introduction to Linear Algebra Gilbert Strang
martes, 28 de septiembre de 2010
Suscribirse a:
Entradas (Atom)