Métodos numéricos
La disciplina ocupada de describir, analizar y crear algoritmos numéricos que nos permitan resolver problemas matemáticos, en los que estén involucradas cantidades numéricas
En el contexto del cálculo numérico, un algoritmo es un procedimiento que nos puede llevar a una solución aproximada de un problema mediante un número finito de pasos que pueden ejecutarse de manera lógica.
A partir de aquí, aparece un concepto adicional, el de error.
Búsqueda de raíces
En análisis numérico un algoritmo de búsqueda de raíces es un método numérico o algoritmo para encontrar las soluciones aproximadas de una ecuación dada por la expresión f(x) = 0 para una función matemática f dada. A la solución x de la ecuación se le llama raíz o cero de la función.
El algoritmo más simple de búsqueda de raíces es el método de bisección. Requiere un intervalo inicial que contenga alguna raíz de la ecuación (de forma que la función tome en los extremos del mismo valores de distinto signo; véase el teorema de Bolzano). Dicho intervalo inicial se va dividiendo sucesivamente por la mitad (se bisecta) tomándose el intervalo que contiene a la raíz. A pesar de ser un método que siempre converge a una solución, converge muy lentamente.
http://es.wikipedia.org/wiki/M%C3%A9todo_de_bisecci%C3%B3n
Ejemplo función:
f(x)=x^2-1 Entre el 0 y 3
Ejemplo función:
f(x)=x^2+x-1 Entre 0 y 1
Es un algoritmo seguro pero lento
Uno mejor: Método de Newton
http://es.wikipedia.org/wiki/M%C3%A9todo_de_Newton
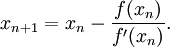
Ejemplo función
f(x)=x^2-1 Entre el 0 y 3
Ejemplo función
f(x)=x^2+x-1 Entre 0 y 1
La disciplina ocupada de describir, analizar y crear algoritmos numéricos que nos permitan resolver problemas matemáticos, en los que estén involucradas cantidades numéricas
En el contexto del cálculo numérico, un algoritmo es un procedimiento que nos puede llevar a una solución aproximada de un problema mediante un número finito de pasos que pueden ejecutarse de manera lógica.
A partir de aquí, aparece un concepto adicional, el de error.
Búsqueda de raíces
En análisis numérico un algoritmo de búsqueda de raíces es un método numérico o algoritmo para encontrar las soluciones aproximadas de una ecuación dada por la expresión f(x) = 0 para una función matemática f dada. A la solución x de la ecuación se le llama raíz o cero de la función.
El algoritmo más simple de búsqueda de raíces es el método de bisección. Requiere un intervalo inicial que contenga alguna raíz de la ecuación (de forma que la función tome en los extremos del mismo valores de distinto signo; véase el teorema de Bolzano). Dicho intervalo inicial se va dividiendo sucesivamente por la mitad (se bisecta) tomándose el intervalo que contiene a la raíz. A pesar de ser un método que siempre converge a una solución, converge muy lentamente.
http://es.wikipedia.org/wiki/M%C3%A9todo_de_bisecci%C3%B3n
Ejemplo función:
f(x)=x^2-1 Entre el 0 y 3
Ejemplo función:
f(x)=x^2+x-1 Entre 0 y 1
Es un algoritmo seguro pero lento
Uno mejor: Método de Newton
http://es.wikipedia.org/wiki/M%C3%A9todo_de_Newton
Ejemplo función
f(x)=x^2-1 Entre el 0 y 3
Ejemplo función
f(x)=x^2+x-1 Entre 0 y 1
No hay comentarios:
Publicar un comentario