1º Tarea (La práctica de ordenador). Cuando terminéis la práctica mandarme un correo a pcampillo@goumh.umh.es
2º Había un ejercicio de métodos numéricos. Hay que mandar los resultados a pcampillo@goumh.umh.es
3º Había otro ejercicio de métodos numéricos. Hay que mandar los resultados a pcampillo@goumh.umh.es
4º Sobre lo de hacer un post, de momento es imposible, no están funcionando las cuentas goumh, para hacer blog. "de momento".
martes, 28 de diciembre de 2010
domingo, 26 de diciembre de 2010
lunes, 20 de diciembre de 2010
2º Parcial Corregido Parcial del 18-12-2010
Los alumnos que quieran ver, recoger el 2º Parcial, estaré en mi despacho a a partir de las 11:20
jueves, 16 de diciembre de 2010
Las soluciones que me salen de los ejercicios CUIDADO HOJA RECTIFICADA
1º Ejercicio Solución 6'8 segundos
2º Ejercicio Solución 172 segundos
3º Nota la función que definía la región estaba equivocada en la hoja y la he tenido que cambiar
Solución 0,533
4º Solución 0'183
5º Rectificación en la función para que tome valores positivos
Mediana 1º Paso 4, 2º Paso 5.5
Trapecio 1º Paso 10, 2º Paso 7
NOTA: He hecho los ejercicios, pero puede ser que me haya equivocado (suele ser habitual)
2º Ejercicio Solución 172 segundos
3º Nota la función que definía la región estaba equivocada en la hoja y la he tenido que cambiar
Solución 0,533
4º Solución 0'183
5º Rectificación en la función para que tome valores positivos
Mediana 1º Paso 4, 2º Paso 5.5
Trapecio 1º Paso 10, 2º Paso 7
NOTA: He hecho los ejercicios, pero puede ser que me haya equivocado (suele ser habitual)
Clases del Miércoles 15 de Diciembre y Jueves 16 de Diciembre
Las clases del Miércoles 15 de Diciembre y Jueves 16 de Diciembre
Han sido talleres de ejercicios para preparar el 2º Parcial de la asignatura.
Han sido talleres de ejercicios para preparar el 2º Parcial de la asignatura.
miércoles, 15 de diciembre de 2010
PLES
El Martes pasado estuve en las Jornadas de Inovación docente de la UMH. Y Jordi Adell nos hablo de los PLES, os dejo un vídeo de 10 minutos.
A lo mejor esta navidad hacemos algo de esto ????
Cuando digo hacemos, me refiero a alumnos y profesor.
TEMA PRACTICAS ORDENADOR
A medida que vayáis terminado las prácticas de ordenador, ir enviándome un correo a pcampillo@goumh.umh.es que vaya corrigiendo.
viernes, 10 de diciembre de 2010
Versión 0.1 Parcial
Primera parte
1º Complejo
2º Problema de métodos numéricos.
3º Diagonalización de matrices.
Segunda parte
4º Factorización LU
5º Problema de ecuaciones diferenciales
6º Calculo de Área o Volúmenes mediante integrales
7º Integrales dobles o Integrales Triples
1º Complejo
2º Problema de métodos numéricos.
3º Diagonalización de matrices.
Segunda parte
4º Factorización LU
5º Problema de ecuaciones diferenciales
6º Calculo de Área o Volúmenes mediante integrales
7º Integrales dobles o Integrales Triples
Clase del 10 de Diciembre del 2010
Métodos numéricos
Calculo de Integrales mediante metodos númericos
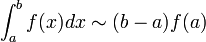
Regla del rectángulo
El método más simple de este tipo es hacer a la función interpoladora ser una función constante (un polinomio de orden cero) que pasa a través del punto (a,f(a)). Este método se llama la regla del rectángulo:Regla del punto medio
Si en el método anterior la función pasa a través del punto
regla del punto medio:
Regla del trapecio
La función interpoladora puede ser una función afín (un polinomio de grado 1 o sea una recta) que pasa a través de los puntos 
regla del trapecio:
regla del trapecio:
Regla de Simpson
La función interpoladora puede ser un polinomio de grado 2 que pasa a través de los puntos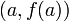 
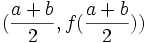
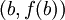
Ejercicio para hacer y entregar
intervalo [0,2] , por todos los métodos estudiados, primero con un solo intervalo, y después haciendo dos intervalos.Enviar los resultados a pcampillo@goumh.umh.es
jueves, 9 de diciembre de 2010
Clase del 9 de Diciembre del 2010 Métodos numéricos
Métodos numéricos
La disciplina ocupada de describir, analizar y crear algoritmos numéricos que nos permitan resolver problemas matemáticos, en los que estén involucradas cantidades numéricas
En el contexto del cálculo numérico, un algoritmo es un procedimiento que nos puede llevar a una solución aproximada de un problema mediante un número finito de pasos que pueden ejecutarse de manera lógica.
A partir de aquí, aparece un concepto adicional, el de error.
Búsqueda de raíces
En análisis numérico un algoritmo de búsqueda de raíces es un método numérico o algoritmo para encontrar las soluciones aproximadas de una ecuación dada por la expresión f(x) = 0 para una función matemática f dada. A la solución x de la ecuación se le llama raíz o cero de la función.
El algoritmo más simple de búsqueda de raíces es el método de bisección. Requiere un intervalo inicial que contenga alguna raíz de la ecuación (de forma que la función tome en los extremos del mismo valores de distinto signo; véase el teorema de Bolzano). Dicho intervalo inicial se va dividiendo sucesivamente por la mitad (se bisecta) tomándose el intervalo que contiene a la raíz. A pesar de ser un método que siempre converge a una solución, converge muy lentamente.
http://es.wikipedia.org/wiki/M%C3%A9todo_de_bisecci%C3%B3n
Ejemplo función:
f(x)=x^2-1 Entre el 0 y 3
Ejemplo función:
f(x)=x^2+x-1 Entre 0 y 1
Es un algoritmo seguro pero lento
Uno mejor: Método de Newton
http://es.wikipedia.org/wiki/M%C3%A9todo_de_Newton
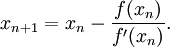
Ejemplo función
f(x)=x^2-1 Entre el 0 y 3
Ejemplo función
f(x)=x^2+x-1 Entre 0 y 1
La disciplina ocupada de describir, analizar y crear algoritmos numéricos que nos permitan resolver problemas matemáticos, en los que estén involucradas cantidades numéricas
En el contexto del cálculo numérico, un algoritmo es un procedimiento que nos puede llevar a una solución aproximada de un problema mediante un número finito de pasos que pueden ejecutarse de manera lógica.
A partir de aquí, aparece un concepto adicional, el de error.
Búsqueda de raíces
En análisis numérico un algoritmo de búsqueda de raíces es un método numérico o algoritmo para encontrar las soluciones aproximadas de una ecuación dada por la expresión f(x) = 0 para una función matemática f dada. A la solución x de la ecuación se le llama raíz o cero de la función.
El algoritmo más simple de búsqueda de raíces es el método de bisección. Requiere un intervalo inicial que contenga alguna raíz de la ecuación (de forma que la función tome en los extremos del mismo valores de distinto signo; véase el teorema de Bolzano). Dicho intervalo inicial se va dividiendo sucesivamente por la mitad (se bisecta) tomándose el intervalo que contiene a la raíz. A pesar de ser un método que siempre converge a una solución, converge muy lentamente.
http://es.wikipedia.org/wiki/M%C3%A9todo_de_bisecci%C3%B3n
Ejemplo función:
f(x)=x^2-1 Entre el 0 y 3
Ejemplo función:
f(x)=x^2+x-1 Entre 0 y 1
Es un algoritmo seguro pero lento
Uno mejor: Método de Newton
http://es.wikipedia.org/wiki/M%C3%A9todo_de_Newton
Ejemplo función
f(x)=x^2-1 Entre el 0 y 3
Ejemplo función
f(x)=x^2+x-1 Entre 0 y 1
lunes, 6 de diciembre de 2010
Practicas de Ordenador
Os recomiendo que abráis el documento que podéis encontrar pinchando en BORRADOR y que lo seleccionéis todo y lo copiéis en otro documento propio.
El otro documento debe de ser un Google Doc,
Para ello entrar en docs.goumh.umh.es
Os pedirá vuestro nombre de usuario y contraseña, tenéis que hacer lo mismo que habéis hecho habitualmente en Clase de Informática.
Vuestro nombre de usuario es (lo que hay delante de la arroba, de vuestro correo de la universidad) y vuestra clave, es el PIN que os dieron al realizar la matricula.
Es entonces cuando tenéis que hacer un documento nuevo en Google Doc, donde haréis la practica.
En ese documento copiareis lo que poner en el documento BORRADOR para facilitar el copiar os digo los comandos que debéis de utilizar.
Ctrl+A para seleccionar todo el documento
Ctrl+C para copiar
Ctrl +V para pegar
Después tenéis que compartir el documento con pcampillo@goumh.umh.es
Las practicas estan divididas en 2 ejercicios.
El primero se basa en las características que tiene Google como calculadora y conversor
El segundo se basa en las posibilidades de Wolfranalpha como asistente matemático.
El otro documento debe de ser un Google Doc,
Para ello entrar en docs.goumh.umh.es
Os pedirá vuestro nombre de usuario y contraseña, tenéis que hacer lo mismo que habéis hecho habitualmente en Clase de Informática.
Vuestro nombre de usuario es (lo que hay delante de la arroba, de vuestro correo de la universidad) y vuestra clave, es el PIN que os dieron al realizar la matricula.
Es entonces cuando tenéis que hacer un documento nuevo en Google Doc, donde haréis la practica.
En ese documento copiareis lo que poner en el documento BORRADOR para facilitar el copiar os digo los comandos que debéis de utilizar.
Ctrl+A para seleccionar todo el documento
Ctrl+C para copiar
Ctrl +V para pegar
Después tenéis que compartir el documento con pcampillo@goumh.umh.es
Las practicas estan divididas en 2 ejercicios.
El primero se basa en las características que tiene Google como calculadora y conversor
El segundo se basa en las posibilidades de Wolfranalpha como asistente matemático.
Clase del 2-12-2010 Viernes
Ejemplo de calculo del Área de una función entre dos curvas. Integrales de 1 variable
Ejemplo de Integral de una función de dos variables sobre un recinto, Integrales dobles. Calculo del Volumen
Ejemplo de Integrales triples.
Practicas en el aula de Informática
Ejemplo de Integral de una función de dos variables sobre un recinto, Integrales dobles. Calculo del Volumen
Ejemplo de Integrales triples.
Practicas en el aula de Informática
miércoles, 1 de diciembre de 2010
Suscribirse a:
Entradas (Atom)